【论文笔记】Emerging Properties in Self-Supervised Vision Transformers

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 16k 阅读时长 ≈ 59 分钟
In this paper, we question if self-supervised learning provides new properties to Vision Transformer (ViT) that stand out compared to convolutional networks (convnets). Beyond the fact that adapting self-supervised methods to this architecture works particularly well, we make the following observations: first, self-supervised ViT features contain explicit information about the semantic segmentation of an image, which does not emerge as clearly with supervised ViTs, nor with convnets. Second, these features are also excellent $k$-NN classifiers, reaching 78.3% top-1 on ImageNet with a small ViT. Our study also underlines the importance of momentum encoder, multi-crop training, and the use of small patches with ViTs. We implement our findings into a simple self-supervised method, called DINO, which we interpret as a form of self-distillation with no labels. We show the synergy between DINO and ViTs by achieving 80.1% top-1 on ImageNet in linear evaluation with ViT-Base.

Emerging Properties in Self-Supervised Vision Transformers

Figure 1: Self-attention from a Vision Transformer with 8 \times 8 patches trained with no supervision. We look at the self-attention of the [CLS] token on the heads of the last layer. This token is not attached to any label nor supervision. These maps show that the model automatically learns class-specific features leading to unsupervised object segmentations.

Abstract

1. Introduction

3. Approach

"Talk is cheap. Show me the code."

― Linus Torvalds

DINO的原仓库给出了一个demo：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
# Copyright (c) Facebook, Inc. and its affiliates.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#     http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import os
import sys
import argparse
import cv2
import random
import colorsys
import requests
from io import BytesIO

import skimage.io
from skimage.measure import find_contours
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
import torch
import torch.nn as nn
import torchvision
from torchvision import transforms as pth_transforms
import numpy as np
from PIL import Image

import utils
import vision_transformer as vits


def apply_mask(image, mask, color, alpha=0.5):
    for c in range(3):
        image[:, :, c] = image[:, :, c] * (1 - alpha * mask) + alpha * mask * color[c] * 255
    return image


def random_colors(N, bright=True):
    """
    Generate random colors.
    """
    brightness = 1.0 if bright else 0.7
    hsv = [(i / N, 1, brightness) for i in range(N)]
    colors = list(map(lambda c: colorsys.hsv_to_rgb(*c), hsv))
    random.shuffle(colors)
    return colors


def display_instances(image, mask, fname="test", figsize=(5, 5), blur=False, contour=True, alpha=0.5):
    fig = plt.figure(figsize=figsize, frameon=False)
    ax = plt.Axes(fig, [0., 0., 1., 1.])
    ax.set_axis_off()
    fig.add_axes(ax)
    ax = plt.gca()

    N = 1
    mask = mask[None, :, :]
    # Generate random colors
    colors = random_colors(N)

    # Show area outside image boundaries.
    height, width = image.shape[:2]
    margin = 0
    ax.set_ylim(height + margin, -margin)
    ax.set_xlim(-margin, width + margin)
    ax.axis('off')
    masked_image = image.astype(np.uint32).copy()
    for i in range(N):
        color = colors[i]
        _mask = mask[i]
        if blur:
            _mask = cv2.blur(_mask,(10,10))
        # Mask
        masked_image = apply_mask(masked_image, _mask, color, alpha)
        # Mask Polygon
        # Pad to ensure proper polygons for masks that touch image edges.
        if contour:
            padded_mask = np.zeros((_mask.shape[0] + 2, _mask.shape[1] + 2))
            padded_mask[1:-1, 1:-1] = _mask
            contours = find_contours(padded_mask, 0.5)
            for verts in contours:
                # Subtract the padding and flip (y, x) to (x, y)
                verts = np.fliplr(verts) - 1
                p = Polygon(verts, facecolor="none", edgecolor=color)
                ax.add_patch(p)
    ax.imshow(masked_image.astype(np.uint8), aspect='auto')
    fig.savefig(fname)
    print(f"{fname} saved.")
    return


if __name__ == '__main__':
    parser = argparse.ArgumentParser('Visualize Self-Attention maps')
    parser.add_argument('--arch', default='vit_small', type=str,
        choices=['vit_tiny', 'vit_small', 'vit_base'], help='Architecture (support only ViT atm).')
    parser.add_argument('--patch_size', default=8, type=int, help='Patch resolution of the model.')
    parser.add_argument('--pretrained_weights', default='', type=str,
        help="Path to pretrained weights to load.")
    parser.add_argument("--checkpoint_key", default="teacher", type=str,
        help='Key to use in the checkpoint (example: "teacher")')
    parser.add_argument("--image_path", default=None, type=str, help="Path of the image to load.")
    parser.add_argument("--image_size", default=(480, 480), type=int, nargs="+", help="Resize image.")
    parser.add_argument('--output_dir', default='.', help='Path where to save visualizations.')
    parser.add_argument("--threshold", type=float, default=None, help="""We visualize masks
        obtained by thresholding the self-attention maps to keep xx% of the mass.""")
    args = parser.parse_args()

    device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
    # build model
    model = vits.__dict__[args.arch](patch_size=args.patch_size, num_classes=0)
    for p in model.parameters():
        p.requires_grad = False
    model.eval()
    model.to(device)
    if os.path.isfile(args.pretrained_weights):
        state_dict = torch.load(args.pretrained_weights, map_location="cpu")
        if args.checkpoint_key is not None and args.checkpoint_key in state_dict:
            print(f"Take key {args.checkpoint_key} in provided checkpoint dict")
            state_dict = state_dict[args.checkpoint_key]
        # remove `module.` prefix
        state_dict = {k.replace("module.", ""): v for k, v in state_dict.items()}
        # remove `backbone.` prefix induced by multicrop wrapper
        state_dict = {k.replace("backbone.", ""): v for k, v in state_dict.items()}
        msg = model.load_state_dict(state_dict, strict=False)
        print('Pretrained weights found at {} and loaded with msg: {}'.format(args.pretrained_weights, msg))
    else:
        print("Please use the `--pretrained_weights` argument to indicate the path of the checkpoint to evaluate.")
        url = None
        if args.arch == "vit_small" and args.patch_size == 16:
            url = "dino_deitsmall16_pretrain/dino_deitsmall16_pretrain.pth"
        elif args.arch == "vit_small" and args.patch_size == 8:
            url = "dino_deitsmall8_300ep_pretrain/dino_deitsmall8_300ep_pretrain.pth"  # model used for visualizations in our paper
        elif args.arch == "vit_base" and args.patch_size == 16:
            url = "dino_vitbase16_pretrain/dino_vitbase16_pretrain.pth"
        elif args.arch == "vit_base" and args.patch_size == 8:
            url = "dino_vitbase8_pretrain/dino_vitbase8_pretrain.pth"
        if url is not None:
            print("Since no pretrained weights have been provided, we load the reference pretrained DINO weights.")
            state_dict = torch.hub.load_state_dict_from_url(url="https://dl.fbaipublicfiles.com/dino/" + url)
            model.load_state_dict(state_dict, strict=True)
        else:
            print("There is no reference weights available for this model => We use random weights.")

    # open image
    if args.image_path is None:
        # user has not specified any image - we use our own image
        print("Please use the `--image_path` argument to indicate the path of the image you wish to visualize.")
        print("Since no image path have been provided, we take the first image in our paper.")
        response = requests.get("https://dl.fbaipublicfiles.com/dino/img.png")
        img = Image.open(BytesIO(response.content))
        img = img.convert('RGB')
    elif os.path.isfile(args.image_path):
        with open(args.image_path, 'rb') as f:
            img = Image.open(f)
            img = img.convert('RGB')
    else:
        print(f"Provided image path {args.image_path} is non valid.")
        sys.exit(1)
    transform = pth_transforms.Compose([
        pth_transforms.Resize(args.image_size),
        pth_transforms.ToTensor(),
        pth_transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225)),
    ])
    img = transform(img)

    # make the image divisible by the patch size
    w, h = img.shape[1] - img.shape[1] % args.patch_size, img.shape[2] - img.shape[2] % args.patch_size
    img = img[:, :w, :h].unsqueeze(0)

    w_featmap = img.shape[-2] // args.patch_size
    h_featmap = img.shape[-1] // args.patch_size

    attentions = model.get_last_selfattention(img.to(device))

    nh = attentions.shape[1] # number of head

    # we keep only the output patch attention
    attentions = attentions[0, :, 0, 1:].reshape(nh, -1)

    if args.threshold is not None:
        # we keep only a certain percentage of the mass
        val, idx = torch.sort(attentions)
        val /= torch.sum(val, dim=1, keepdim=True)
        cumval = torch.cumsum(val, dim=1)
        th_attn = cumval > (1 - args.threshold)
        idx2 = torch.argsort(idx)
        for head in range(nh):
            th_attn[head] = th_attn[head][idx2[head]]
        th_attn = th_attn.reshape(nh, w_featmap, h_featmap).float()
        # interpolate
        th_attn = nn.functional.interpolate(th_attn.unsqueeze(0), scale_factor=args.patch_size, mode="nearest")[0].cpu().numpy()

    attentions = attentions.reshape(nh, w_featmap, h_featmap)
    attentions = nn.functional.interpolate(attentions.unsqueeze(0), scale_factor=args.patch_size, mode="nearest")[0].cpu().numpy()

    # save attentions heatmaps
    os.makedirs(args.output_dir, exist_ok=True)
    torchvision.utils.save_image(torchvision.utils.make_grid(img, normalize=True, scale_each=True), os.path.join(args.output_dir, "img.png"))
    for j in range(nh):
        fname = os.path.join(args.output_dir, "attn-head" + str(j) + ".png")
        plt.imsave(fname=fname, arr=attentions[j], format='png')
        print(f"{fname} saved.")

    if args.threshold is not None:
        image = skimage.io.imread(os.path.join(args.output_dir, "img.png"))
        for j in range(nh):
            display_instances(image, th_attn[j], fname=os.path.join(args.output_dir, "mask_th" + str(args.threshold) + "_head" + str(j) +".png"), blur=False)

同时也给出了这段代码的运行方式：

1
python visualize_attention.py

我们不妨直接运行，其结果如下：

demo-res

其中：

  • demo：表示输入图像；
  • img：表示输入图像经过torchvision.utils.make_grid(img, normalize=True, scale_each=True)函数处理后的图像；
  • attn-head0 - attn-head5：表示第0个注意力头到第5个注意力头的注意力图。

接下来我们逐行分析visualize_attention.py的代码：

  • 1-35行：引入包；

  • 38-41行：定义apply_mask函数，该函数用于将彩色遮罩叠加到原始图像上；

  • 44-52行：定义random_colors函数，该函数用于生成随机颜色，使用HSV颜色空间来确保生成的颜色具有良好的视觉区分度；

  • 55-95行：定义display_instances函数，该函数用于显示和保存带有遮罩的图像；

  • 98-213行：main函数，接下来会详细解释main函数：

    • 99-148行：接收参数、加载模型；
    • 151-170行：读取图像，并对图像进行预处理；
    • 173-174行：make the image divisible by the patch size；
    • 176-177行：获取注意力图的高和宽；
    • 179行：获取所有注意力头的注意力图；
    • 181行：获取注意力头的数量；
    • 184行：在所有注意力头上获取类别标签[CLS]对图像所有patch的注意力向量；
    • 186-197行：如果传入了--threshold参数，则只保留累积注意力值达到阈值的区域这里在运行demo时没有设置--threshold参数，所以没有执行这一段代码，th_attn为空；
    • 199-200行：在所有注意力头上将类别标签[CLS]对图像所有patch的注意力向量reshape成2维图像，假设有\(n\)个注意力头，那么此时有\(n\)个2维图像，在reshape后，使用最近邻nearest插值将注意力图的分辨率恢复到输入图像的分辨率；
    • 203-208行：保存所有注意力头的注意力图；
    • 210-213行：保存186-197行处理后的注意力图。

显然，179行的attentions = model.get_last_selfattention(img.to(device))是整段代码的关键。

get_last_selfattention函数的定义在vision_transformer.py第216行：

1
2
3
4
5
6
7
class VisionTransformer(nn.Module):
    """ Vision Transformer """
    # ... existing code ...
    def get_last_selfattention(self, x):
        x = self.prepare_tokens(x)
        # ... existing code ...
    # ... existing code ...

get_last_selfattention函数在执行时，首先会调用prepare_tokens函数，prepare_tokens函数的定义在vision_transformer.py第196行：

1
2
3
4
5
6
7
8
class VisionTransformer(nn.Module):
    """ Vision Transformer """
    # ... existing code ...
    def prepare_tokens(self, x):
        B, nc, w, h = x.shape
        x = self.patch_embed(x)  # patch linear embedding
        # ... existing code ...
    # ... existing code ...

prepare_tokens函数在执行时，会继续调用patch_embed，patch_embed是PatchEmbed类的实例，PatchEmbed类的定义在vision_transformer.py第116行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class PatchEmbed(nn.Module):
    """ Image to Patch Embedding
    """
    def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768):
        super().__init__()
        num_patches = (img_size // patch_size) * (img_size // patch_size)
        self.img_size = img_size
        self.patch_size = patch_size
        self.num_patches = num_patches

        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

    def forward(self, x):
        B, C, H, W = x.shape
        x = self.proj(x).flatten(2).transpose(1, 2)
        return x

PatchEmbed类继承于nn.Module，所以先看forward函数：

  • B, C, H, W = x.shape是获取了图像的batch_size B、通道数C、图像高度H和图像宽度W；

  • x = self.proj(x).flatten(2).transpose(1, 2)等价于顺序执行下面三步：

    • x = self.proj(x)，x = x.flatten(2)，x = x.transpose(1, 2)；

    • 其中：

      • x = self.proj(x)表示使用卷积核nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)对输入图像进行了处理，in_chans为输入通道数，embed_dim为输出通道数，kernel_size为卷积核大小，stride为步长。这里的embed_dim就是\(D\)，patch_size就是\(P\)，且该卷积操作的卷积核大小和步长大小相同，所以将输入图片经过这个卷积操作后，每一个patch都会被映射成一个\(D\)维的向量，且patch和patch之间没有重合部分，那么最后输出的维度是\(\mathbb{R}^{B \times D \times \frac{H}{P} \times \frac{W}{P}}\)；
      • x = x.flatten(2)表示从x的第2维开始展平，保持维度0和1不变，将维度2和3合并，令\(N = \frac{H}{P} \times \frac{W}{P}\)为patch的数量，那么最后输出的维度是\(\mathbb{R}^{B \times D \times N}\)；
      • x = x.transpose(1, 2)表示将维度1和维度2交换，那么最后输出的维度是\(\mathbb{R}^{B \times N \times D}\)，用卷积核的参数表示，输出的维度为\(\mathbb{R}^{B \times \frac{\text{img_size}^2}{\text{patch_size}^2} \times \text{embed_dim}}\)。

patch_embed类结束，回到prepare_tokens函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class VisionTransformer(nn.Module):
    """ Vision Transformer """
    def __init__(self, img_size=[224], patch_size=16, in_chans=3, num_classes=0, embed_dim=768, depth=12,
                 num_heads=12, mlp_ratio=4., qkv_bias=False, qk_scale=None, drop_rate=0., attn_drop_rate=0.,
                 drop_path_rate=0., norm_layer=nn.LayerNorm, **kwargs):
        # ... existing code ...
        self.cls_token = nn.Parameter(torch.zeros(1, 1, embed_dim))
        # ... existing code ...
        self.pos_drop = nn.Dropout(p=drop_rate)
        # ... existing code ...
        trunc_normal_(self.cls_token, std=.02)
        # ... existing code ...
    # ... existing code ...
    def prepare_tokens(self, x):
        B, nc, w, h = x.shape
        x = self.patch_embed(x)  # patch linear embedding

        # add the [CLS] token to the embed patch tokens
        cls_tokens = self.cls_token.expand(B, -1, -1)
        x = torch.cat((cls_tokens, x), dim=1)

        # add positional encoding to each token
        x = x + self.interpolate_pos_encoding(x, w, h)

        return self.pos_drop(x)
    # ... existing code ...

在执行完x = self.patch_embed(x)后，x的维度为\(\mathbb{R}^{B \times \frac{\text{img_size}^2}{\text{patch_size}^2} \times \text{embed_dim}}\)，self.cls_token的维度为\(\mathbb{R}^{1 \times 1 \times \text{embed_dim}}\)，所以在expand(B, -1, -1)之后，cls_tokens的维度为\(\mathbb{R}^{B \times 1 \times \text{embed_dim}}\)，x = torch.cat((cls_tokens, x), dim=1)表示将cls_tokens和x在第1维上拼接，那么最后x的维度为\(\mathbb{R}^{B \times \left(\frac{\text{img_size}^2}{\text{patch_size}^2} + 1\right) \times \text{embed_dim}}\)。

reshape做完，线性映射完，[CLS]拼接完，接下来是位置编码，即x = x + self.interpolate_pos_encoding(x, w, h)，interpolate_pos_encoding函数的定义在vision_transformer.py第174行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class VisionTransformer(nn.Module):
    """ Vision Transformer """
    # ... existing code ...
    def __init__(self, img_size=[224], patch_size=16, in_chans=3, num_classes=0, embed_dim=768, depth=12,
                 num_heads=12, mlp_ratio=4., qkv_bias=False, qk_scale=None, drop_rate=0., attn_drop_rate=0.,
                 drop_path_rate=0., norm_layer=nn.LayerNorm, **kwargs):
        # ... existing code ...
        self.pos_embed = nn.Parameter(torch.zeros(1, num_patches + 1, embed_dim))
        # ... existing code ...
        trunc_normal_(self.pos_embed, std=.02)
        # ... existing code ...
    # ... existing code ...
    def interpolate_pos_encoding(self, x, w, h):
        npatch = x.shape[1] - 1
        N = self.pos_embed.shape[1] - 1
        if npatch == N and w == h:
            return self.pos_embed
        class_pos_embed = self.pos_embed[:, 0]
        patch_pos_embed = self.pos_embed[:, 1:]
        dim = x.shape[-1]
        w0 = w // self.patch_embed.patch_size
        h0 = h // self.patch_embed.patch_size
        # we add a small number to avoid floating point error in the interpolation
        # see discussion at https://github.com/facebookresearch/dino/issues/8
        w0, h0 = w0 + 0.1, h0 + 0.1
        patch_pos_embed = nn.functional.interpolate(
            patch_pos_embed.reshape(1, int(math.sqrt(N)), int(math.sqrt(N)), dim).permute(0, 3, 1, 2),
            scale_factor=(w0 / math.sqrt(N), h0 / math.sqrt(N)),
            mode='bicubic',
        )
        assert int(w0) == patch_pos_embed.shape[-2] and int(h0) == patch_pos_embed.shape[-1]
        patch_pos_embed = patch_pos_embed.permute(0, 2, 3, 1).view(1, -1, dim)
        return torch.cat((class_pos_embed.unsqueeze(0), patch_pos_embed), dim=1)
    # ... existing code ...

简单来说，这个函数能够基于初始化生成的位置编码，用插值的方法为不同分辨率的输入图像生成对应的位置编码，以让模型能够处理不同尺寸的输入图像。

最后，返回self.pos_drop(x)，pos_drop函数就是一个简单的nn.Dropout，所以最后x的维度为\(\mathbb{R}^{B \times \left(\frac{\text{img_size}^2}{\text{patch_size}^2} + 1\right) \times \text{embed_dim}}\)。

prepare_tokens函数结束，回到get_last_selfattention函数：

1
2
3
4
5
6
7
8
9
10
11
12
class VisionTransformer(nn.Module):
    """ Vision Transformer """
    # ... existing code ...
    def get_last_selfattention(self, x):
        x = self.prepare_tokens(x)
        for i, blk in enumerate(self.blocks):
            if i < len(self.blocks) - 1:
                x = blk(x)
            else:
                # return attention of the last block
                return blk(x, return_attention=True)
    # ... existing code ...

简单来说，在准备完tokens即x = self.prepare_tokens(x)执行结束后，让x逐个通过所有的self.blocks，当到达最后一个block时，返回最后一个block的注意力图。

那么现在需要知道self.blocks是什么，self.blocks是一个nn.ModuleList，其中包含depth个Block类，Block类的定义在vision_transformer.py第95行：

1
2
3
4
5
6
7
8
9
10
class Block(nn.Module):
    def __init__(self, dim, num_heads, mlp_ratio=4., qkv_bias=False, qk_scale=None, drop=0., attn_drop=0.,
                 drop_path=0., act_layer=nn.GELU, norm_layer=nn.LayerNorm):
        # ... existing code ...
        self.attn = Attention(
            dim, num_heads=num_heads, qkv_bias=qkv_bias, qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
        # ... existing code ...

    def forward(self, x, return_attention=False):
        # ... existing code ...

Block类的核心部分便是Attention类，而Attention类的定义在vision_transformer.py第68行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Attention(nn.Module):
    def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5

        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)

    def forward(self, x):
        B, N, C = x.shape
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        q, k, v = qkv[0], qkv[1], qkv[2]

        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x, attn

在这个Attention类中，同时实现了单头注意力和多头注意力，逐行进行分析：

  • def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):

    1. super().__init__()：调用父类nn.Module的构造函数；
    2. self.num_heads = num_heads：设置注意力头的数量；
    3. head_dim = dim // num_heads：设置每个注意力头所需要处理的特征维度；
    4. self.scale = qk_scale or head_dim ** -0.5：设置注意力分数的缩放因子，如果qk_scale不为空，则使用qk_scale，否则使用head_dim的负0.5次方作为缩放因子，即\(\frac{1}{\sqrt{\text{head_dim}}}\)，和原版Transformer中的设置一致；
    5. self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)：定义一个线性层，将原本的特征维度从C变为3 * C，以便于在后续切分为q, k, v；
    6. self.attn_drop = nn.Dropout(attn_drop)：注意力Dropout；
    7. self.proj = nn.Linear(dim, dim)：一个线性层；
    8. self.proj_drop = nn.Dropout(proj_drop)：投影Dropout；

  • def forward(self, x):

    1. B, N, C = x.shape：获取输入张量的维度，B表示批量大小，N表示序列长度，C表示特征维度，也就是说\(\mathbf{x} \in \mathbb{R}^{B \times N \times C}\)；

    2. qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)：等价于顺序执行下面三步：

      • qkv = self.qkv(x)，qkv = qkv.reshape(B, N, 3, self.num_heads, C // self.num_heads)，qkv = qkv.permute(2, 0, 3, 1, 4)；

      • 其中：

        • qkv = self.qkv(x)：\(\mathbf{qkv} \in \mathbb{R}^{B \times N \times 3C}\)；
        • qkv = qkv.reshape(B, N, 3, self.num_heads, C // self.num_heads)：\(\mathbf{qkv} \in \mathbb{R}^{B \times N \times 3 \times \text{num_heads} \times \frac{C}{\text{num_heads}}}\)；
        • qkv = qkv.permute(2, 0, 3, 1, 4)：\(\mathbf{qkv} \in \mathbb{R}^{3 \times B \times \text{num_heads} \times N \times \frac{C}{\text{num_heads}}}\)；

    3. q, k, v = qkv[0], qkv[1], qkv[2]：

      • \(\mathbf{q} \in \mathbb{R}^{B \times \text{num_heads} \times N \times \frac{C}{\text{num_heads}}}\)；
      • \(\mathbf{k} \in \mathbb{R}^{B \times \text{num_heads} \times N \times \frac{C}{\text{num_heads}}}\)；
      • \(\mathbf{v} \in \mathbb{R}^{B \times \text{num_heads} \times N \times \frac{C}{\text{num_heads}}}\)；

    4. attn = (q @ k.transpose(-2, -1)) * self.scale：\(\mathbf{attn} \in \mathbb{R}^{B \times \text{num_heads} \times N \times N}\)；

    5. attn = attn.softmax(dim=-1)：softmax归一化；

    6. attn = self.attn_drop(attn)：注意力Dropout；

    7. x = (attn @ v).transpose(1, 2).reshape(B, N, C)：等价于顺序执行下面三步：

      • x = (attn @ v)，x = x.transpose(1, 2)，x = x.reshape(B, N, C)；

      • 其中：

        • x = (attn @ v)：\(\mathbf{x} \in \mathbb{R}^{B \times \text{num_heads} \times N \times \frac{C}{\text{num_heads}}}\)；
        • x = x.transpose(1, 2)：\(\mathbf{x} \in \mathbb{R}^{B \times N \times \text{num_heads} \times \frac{C}{\text{num_heads}}}\)；
        • x = x.reshape(B, N, C)：\(\mathbf{x} \in \mathbb{R}^{B \times N \times C}\)；

    8. x = self.proj(x)：\(\mathbf{x} \in \mathbb{R}^{B \times N \times C}\)；

    9. x = self.proj_drop(x)：投影Dropout；

    10. return x, attn：

      • \(\mathbf{x} \in \mathbb{R}^{B \times N \times C}\)；
      • \(\mathbf{attn} \in \mathbb{R}^{B \times \text{num_heads} \times N \times N}\)。

Attention类结束，回到Block类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Block(nn.Module):
    def __init__(self, dim, num_heads, mlp_ratio=4., qkv_bias=False, qk_scale=None, drop=0., attn_drop=0.,
                 drop_path=0., act_layer=nn.GELU, norm_layer=nn.LayerNorm):
        super().__init__()
        self.norm1 = norm_layer(dim)
        self.attn = Attention(
            dim, num_heads=num_heads, qkv_bias=qkv_bias, qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
        self.norm2 = norm_layer(dim)
        mlp_hidden_dim = int(dim * mlp_ratio)
        self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)

    def forward(self, x, return_attention=False):
        y, attn = self.attn(self.norm1(x))
        if return_attention:
            return attn
        x = x + self.drop_path(y)
        x = x + self.drop_path(self.mlp(self.norm2(x)))
        return x

Block类中关键的就只有self.attn了，所以不详细介绍了，要注意的是在forward中，当return_attention=True时，返回的是注意力图，否则返回的是输入经过注意力机制后的结果。

Block类结束，回到get_last_selfattention函数，get_last_selfattention函数中只是Block类的堆叠，所以get_last_selfattention函数也结束。

vision_transformer.py文件中还有下面几个部分没有提到：

  • drop_path函数：

    • 该函数值得展开，函数定义在vision_transformer.py第27行：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      def drop_path(x, drop_prob: float = 0., training: bool = False):
          if drop_prob == 0. or not training:
              return x
          keep_prob = 1 - drop_prob
          shape = (x.shape[0],) + (1,) * (x.ndim - 1)  # work with diff dim tensors, not just 2D ConvNets
          random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
          random_tensor.floor_()  # binarize
          output = x.div(keep_prob) * random_tensor
          return output

      • drop_path，顾名思义，就是丢弃一整条路径上的所有值，但是实际上，drop_path是丢弃输入向量中的若干分量：

        • if drop_prob == 0. or not training: return x：如果drop_prob为0，或者训练模式为False，则直接返回输入向量；
        • keep_prob = 1 - drop_prob：计算保留的概率；
        • shape = (x.shape[0],) + (1,) * (x.ndim - 1)：创建一个与输入张量兼容的广播形状，保持第一维（批次维）不变，其他维度都设为1；
        • random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)：生成一个与输入张量兼容的随机张量，其值在[0 + keep_prob, 1 + keep_prob]之间；
        • random_tensor.floor_()：将随机张量的值向下取整为0或1，相当于二值化；
        • output = x.div(keep_prob) * random_tensor：将输入张量除以保留概率，然后与二值化后的随机张量相乘，得到输出张量；
        • return output：返回输出张量；
        • DropPath与Dropout相比，能够通过缩放保持期望值不变，提供了更好的正则化效果，帮助网络学习更鲁棒的特征；

  • DropPath类：使用drop_path函数处理输入的向量；

  • Mlp类：在Block类中使用到的MLP层；

  • vit_tiny函数：

    1
    2
    3
    4
    5
    def vit_tiny(patch_size=16, **kwargs):
        model = VisionTransformer(
            patch_size=patch_size, embed_dim=192, depth=12, num_heads=3, mlp_ratio=4,
            qkv_bias=True, norm_layer=partial(nn.LayerNorm, eps=1e-6), **kwargs)
        return model

    • mlp_ratio=4：MLP隐藏层维度是嵌入维度的4倍，比如这里MLP隐藏层的维度就是192 * 4 = 768；

  • vit_small函数：

    • embed_dim=384；
    • num_heads=6；

  • vit_base函数：

    • embed_dim=768；
    • num_heads=12；

  • DINOHead类：DINO自监督学习中的特征投影，用于计算学生和教师网络输出的相似度。

还没完，VisionTransformer类中还有下面几个函数没有提到：

  • _init_weights函数：针对不同的层采取不同的初始化方案；
  • forward函数：只输出[CLS] token，用于分类任务；
  • get_intermediate_layers函数：用于获取Vision Transformer最后n个块的中间层特征。

3.1. SSL with Knowledge Distillation

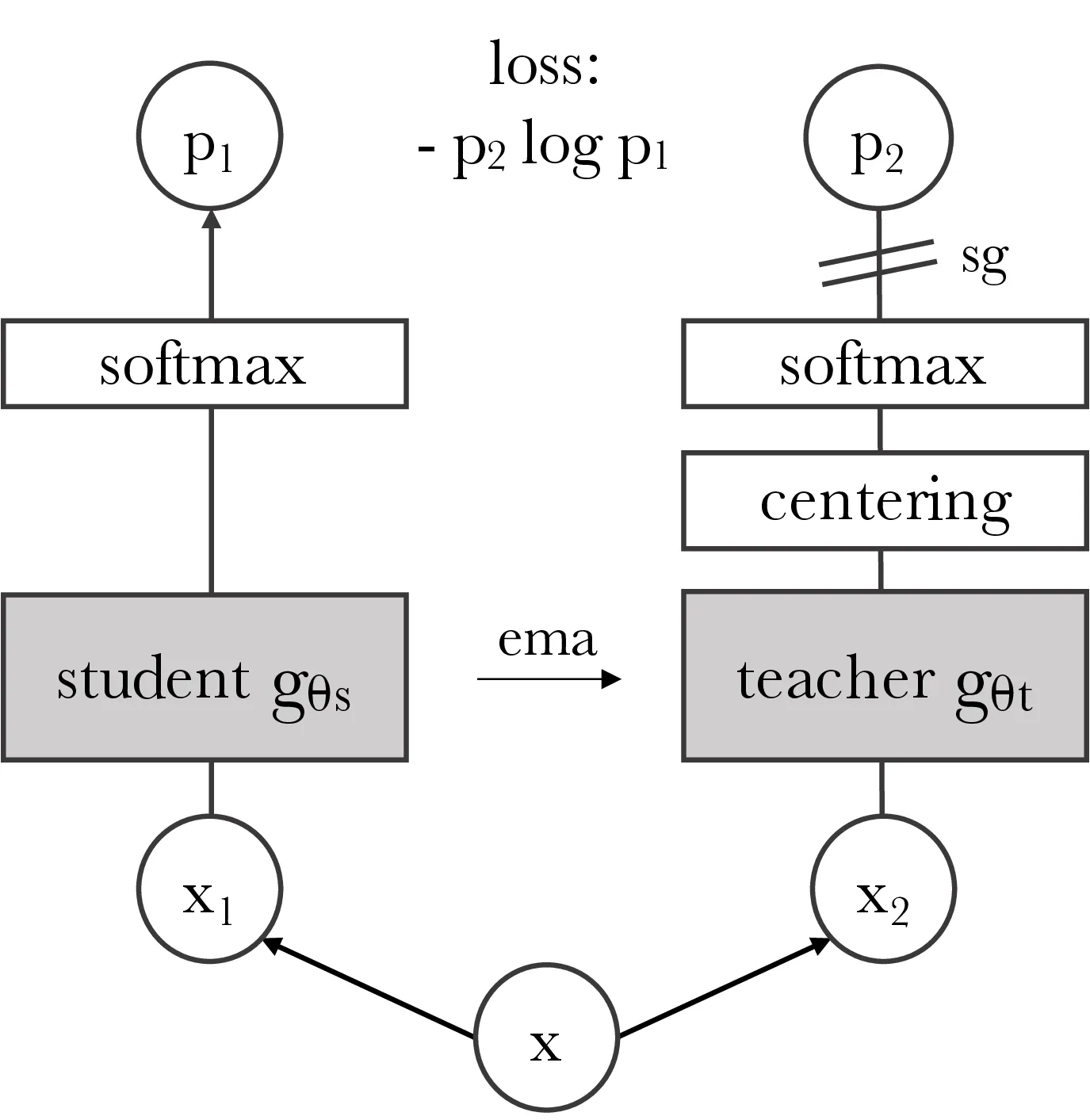
Figure 2: Self-distillation with no labels. We illustrate DINO in the case of one single pair of views (x_1, x_2) for simplicity. The model passes two different random transformations of an input image to the student and teacher networks. Both networks have the same architecture but different parameters. The output of the teacher network is centered with a mean computed over the batch. Each networks outputs a K dimensional feature that is normalized with a temperature softmax over the feature dimension. Their similarity is then measured with a cross-entropy loss. We apply a stop-gradient (sg) operator on the teacher to propagate gradients only through the student. The teacher parameters are updated with an exponential moving average (ema) of the student parameters. 
Algorithm 1 DINO PyTorch pseudocode w/o multi-crop.


# gs, gt: student and teacher networks
# C: center (K)
# tps, tpt: student and teacher temperatures
# l, m: network and center momentum rates
gt.params = gs.params
for x in loader: # load a minibatch x with n samples
    x1, x2 = augment(x), augment(x) # random views

    s1, s2 = gs(x1), gs(x2) # student output n-by-K
    t1, t2 = gt(x1), gt(x2) # teacher output n-by-K

    loss = H(t1, s2)/2 + H(t2, s1)/2
    loss.backward() # back-propagate

    # student, teacher and center updates
    update(gs) # SGD
    gt.params = l*gt.params + (1-l)*gs.params
    C = m*C + (1-m)*cat([t1, t2]).mean(dim=0)

def H(t, s):
    t = t.detach() # stop gradient
    s = softmax(s / tps, dim=1)
    t = softmax((t - C) / tpt, dim=1) # center + sharpen
    return - (t * log(s)).sum(dim=1).mean()

3.2. Implementation and evaluation protocols

Table 1: Networks configuration. "Blocks" is the number of Transformer blocks, "dim" is channel dimension and "heads" is the number of heads in multi-head attention. "# tokens" is the length of the token sequence when considering \(224^2\) resolution inputs, "# params" is the total number of parameters (without counting the projection head) and "im/s" is the inference time on a NVIDIA V100 GPU with 128 samples per forward.
model blocks dim heads #tokens #params im/s
ResNet-50 - 2048 - - 23M 1237
ViT-S/16 12 384 6 197 21M 1007
ViT-S/8 12 384 6 785 21M 180
ViT-B/16 12 768 12 197 85M 312
ViT-B/8 12 768 12 785 85M 63

4. Main Results

4.1. Comparing with SSL frameworks on ImageNet

Table 2: Linear and \(k\)-NN classification on ImageNet. We report top-1 accuracy for linear and \(k\)-NN evaluations on the validation set of ImageNet for different self-supervised methods. We focus on ResNet-50 and ViT-small architectures, but also report the best results obtained across architectures. ∗ are run by us. We run the \(k\)-NN evaluation for models with official released weights. The throughput (im/s) is calculated on a NVIDIA V100 GPU with 128 samples per forward. Parameters (M) are of the feature extractor.
Method Arch. Param. im/s Linear \(k\)-NN
Supervised RN50 23 1237 79.3 79.3
SCLR [12] RN50 23 1237 69.1 60.7
MoCov2 [15] RN50 23 1237 71.1 61.9
InfoMin [67] RN50 23 1237 73.0 65.3
BarlowT [81] RN50 23 1237 73.2 66.0
OBoW [27] RN50 23 1237 73.8 61.9
BYOL [30] RN50 23 1237 74.4 64.8
DCv2 [10] RN50 23 1237 75.2 67.1
SwAV [10] RN50 23 1237 75.3 65.7
DINO RN50 23 1237 75.3 67.5
Supervised ViT-S 21 1007 79.8 79.8
BYOL∗ [30] ViT-S 21 1007 71.4 66.6
MoCov2∗ [15] ViT-S 21 1007 72.7 64.4
SwAV∗ [10] ViT-S 21 1007 73.5 66.3
DINO ViT-S 21 1007 77.0 74.5
Comparison across architectures
SCLR [12] RN50w4 375 117 76.8 69.3
SwAV [10] RN50w2 93 384 77.3 67.3
BYOL [30] RN50w2 93 384 77.4 -
DINO ViT-B/16 85 312 78.2 76.1
SwAV [10] RN50w5 586 76 78.5 67.1
BYOL [30] RN50w4 375 117 78.6 -
BYOL [30] RN200w2 250 123 79.6 73.9
DINO ViT-S/8 21 180 79.7 78.3
SCLRv2 [13] RN152w3+SK 794 46 79.8 73.1
DINO ViT-B/8 85 63 80.1 77.4

4.2. Properties of ViT trained with SSL

4.2.1 Nearest neighbor retrieval with DINO ViT

Figure 3: Attention maps from multiple heads. We consider the heads from the last layer of a ViT-S/8 trained with DINO and display the self-attention for [CLS] token query. Different heads, materialized by different colors, focus on different locations that represents different objects or parts (more examples in Appendix).
Table 3: Image retrieval. We compare the performance in retrieval of off-the-shelf features pretrained with supervision or with DINO on ImageNet and Google Landmarks v2 (GLDv2) dataset. We report mAP on revisited Oxford and Paris. Pretraining with DINO on a landmark dataset performs particularly well. For reference, we also report the best retrieval method with off-the-shelf features [57].
Pretrain Arch. Pretrain \(\mathcal{R}\)Ox \(\mathcal{R}\)Par
M H M H
Sup. [57] RN101+R-MAC ImNet 49.8 18.5 74.0 52.1
Sup. ViT-S/16 ImNet 33.5 8.9 63.0 37.2
DINO ResNet-50 ImNet 35.4 11.1 55.9 27.5
DINO ViT-S/16 ImNet 41.8 13.7 63.1 34.4
DINO ViT-S/16 GLDv2 51.5 24.3 75.3 51.6
Table 4: Copy detection. We report the mAP performance in copy detection on Copydays "strong" subset [21]. For reference, we also report the performance of the multigrain model [5], trained specifically for particular object retrieval.
Method Arch. Dim. Resolution mAP
Multigrain [5] ResNet-50 2048 2242 75.1
Multigrain [5] ResNet-50 2048 largest side 800 82.5
Supervised [69] ViT-B/16 1536 2242 76.4
DINO ViT-B/16 1536 2242 81.7
DINO ViT-B/8 1536 3202 85.5
Table 5: DAVIS 2017 Video object segmentation. We evaluate the quality of frozen features on video instance tracking. We report mean region similarity \(\mathcal{J}_m\) and mean contour-based accuracy \(\mathcal{F}_m\). We compare with existing self-supervised methods and a supervised ViT-S/8 trained on ImageNet. Image resolution is 480p.
Method Data Arch. \((\mathcal{J}\&\mathcal{F})_m\) \(\mathcal{J}_m\) \(\mathcal{F}_m\)
Supervised
ImageNet INet ViT-S/8 66.0 63.9 68.1
STM [48] I/D/Y RN50 81.8 79.2 84.3
Self-supervised
CT [71] VLOG RN50 48.7 46.4 50.0
MAST [40] YT-VOS RN18 65.5 63.3 67.6
STC [37] Kinetics RN18 67.6 64.8 70.2
DINO INet ViT-S/16 61.8 60.2 63.4
DINO INet ViT-B/16 62.3 60.7 63.9
DINO INet ViT-S/8 69.9 66.6 73.1
DINO INet ViT-B/8 71.4 67.9 74.9

4.2.2 Discovering the semantic layout of scenes

4.2.3 Transfer learning on downstream tasks

5. Ablation Study of DINO

5.1. Importance of the Different Components

Random Supervised DINO
ViT-S/16 22.0 27.3 45.9
ViT-S/8 21.8 23.7 44.7
Figure 4: Segmentations from supervised versus DINO. We visualize masks obtained by thresholding the self-attention maps to keep 60% of the mass. On top, we show the resulting masks for a ViT-S/8 trained with supervision and DINO. We show the best head for both models. The table at the bottom compares the Jaccard similarity between the ground truth and these masks on the validation images of PASCAL VOC12 dataset.
Table 6: Transfer learning by finetuning pretrained models on different datasets. We report top-1 accuracy. Self-supervised pretraining with DINO transfers better than supervised pretraining.
Cifar10 Cifar100 INat18 INat19 Flwrs Cars INet
ViT-S/16
Sup. [69] 99.0 89.5 70.7 76.6 98.2 92.1 79.9
DINO 99.0 90.5 72.0 78.2 98.5 93.0 81.5
ViT-B/16
Sup. [69] 99.0 90.8 73.2 77.7 98.4 92.1 81.8
DINO 99.1 91.7 72.6 78.6 98.8 93.0 82.8
Table 7: Important component for self-supervised ViT pre-training. Models are trained for 300 epochs with ViT-S/16. We study the different components that matter for the \(k\)-NN and linear ("Lin.") evaluations. For the different variants, we highlight the differences from the default DINO setting. The best combination is the momentum encoder with the multicrop augmentation and the cross-entropy loss. We also report results with BYOL [30], MoCo-v2 [15] and SwAV [10].
Method Mom. SK MC Loss Pred. \(k\)-NN Lin.
1 DINO ✓ ✗ ✓ CE ✗ 72.8 76.1
2 ✗ ✗ ✓ CE ✗ 0.1 0.1
3 ✓ ✓ ✓ CE ✗ 72.2 76.0
4 ✓ ✗ ✗ CE ✗ 67.9 72.5
5 ✓ ✗ ✓ MSE ✗ 52.6 62.4
6 ✓ ✗ ✓ CE ✓ 71.8 75.6
7 BYOL ✓ ✗ ✗ MSE ✓ 66.6 71.4
8 MoCov2 ✓ ✗ ✗ INCE ✗ 62.0 71.6
9 SwAV ✗ ✓ ✓ CE ✗ 64.7 71.8
SK: Sinkhorn-Knopp, MC: Multi-Crop, Pred.: Predictor
CE: Cross-Entropy, MSE: Mean Square Error, INCE: InfoNCE
Figure 5: Effect of Patch Size. k-NN evaluation as a function of the throughputs for different input patch sizes with ViT-B and ViT-S. Models are trained for 300 epochs.

5.2. Impact of the choice of Teacher Network

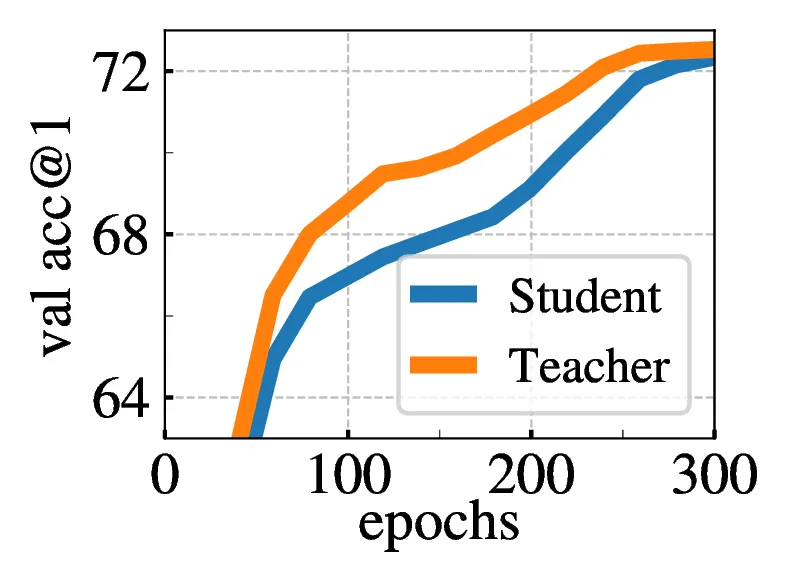
Figure 6: Top-1 accuracy on ImageNet validation with \(k\)-NN classifier. (top) Comparison between the performance of the momentum teacher and the student during training. (bottom) Comparison between different types of teacher network. The momentum encoder leads to the best performance but is not the only viable option.
Teacher Top-1
Student copy 0.1
Previous iter 0.1
Previous epoch 66.6
Momentum 72.8

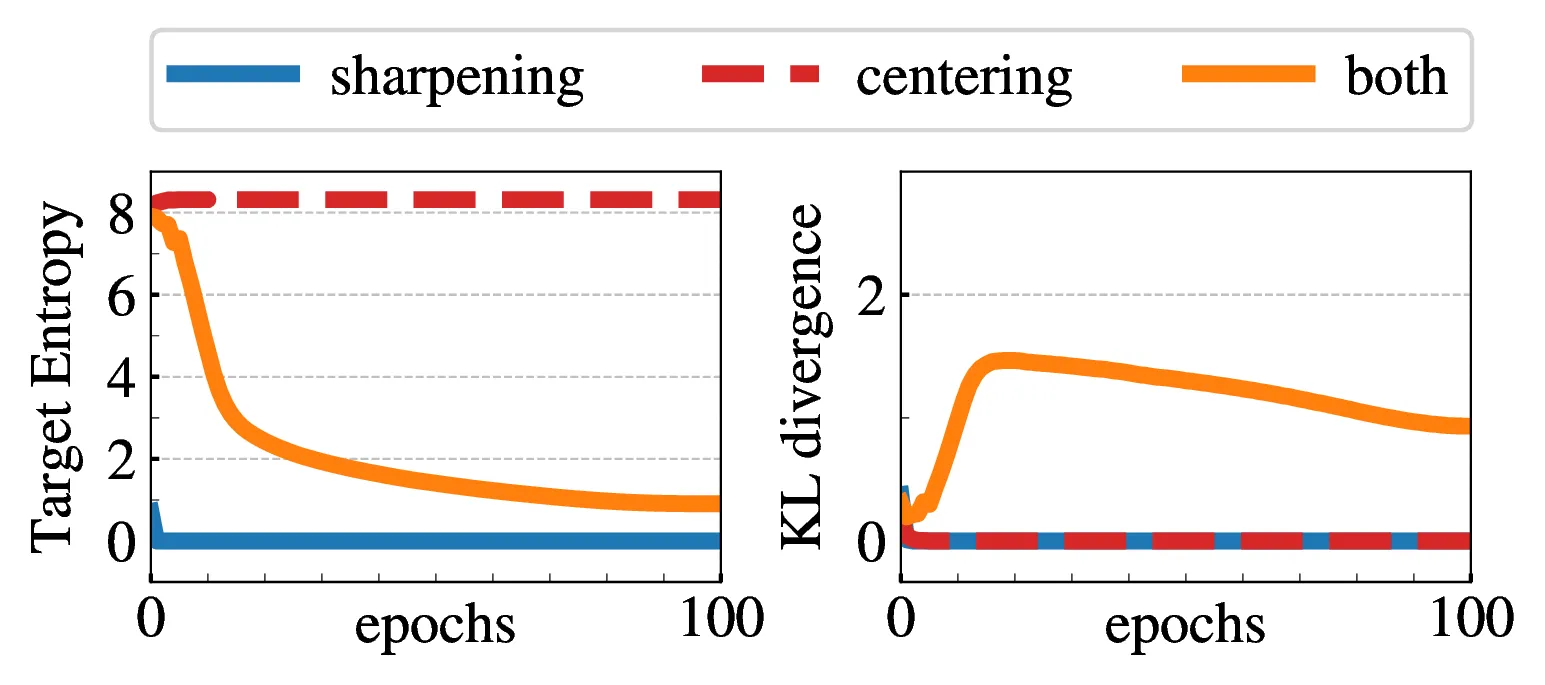
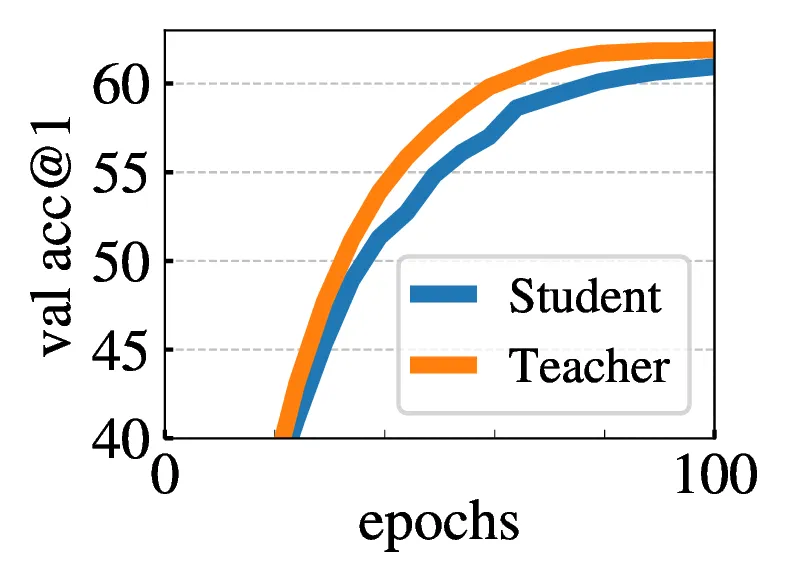
5.3. Avoiding collapse

Figure 7: Collapse study. (left): evolution of the teacher's target entropy along training epochs; (right): evolution of KL divergence between teacher and student outputs.
Table 8: Time and memory requirements. We show total running time and peak memory per GPU ("mem.") when running ViT-S/16 DINO models on two 8-GPU machines. We report top-1 ImageNet val acc with linear evaluation for several variants of multi-crop, each having a different level of compute requirement.
multi-crop 100 epochs 300 epochs mem.
top-1 time top-1 time
2 × 2242 67.8 15.3h 72.5 45.9h 9.3G
2 × 2242 + 2 × 962 71.5 17.0h 74.5 51.0h 10.5G
2 × 2242 + 6 × 962 73.8 20.3h 75.9 60.9h 12.9G
2 × 2242 + 10 × 962 74.6 24.2h 76.1 72.6h 15.4G

5.4. Compute requirements

5.5. Training with small batches

Table 9: Effect of batch sizes. Top-1 with \(k\)-NN for models trained for 100 epochs without multi-crop.
bs 128 256 512 1024
top-1 57.9 59.1 59.6 59.9

Appendix

A. Additional Results

Table 10: \(k\)-NN and linear evaluation for ViT-S/16 and ResNet-50 pre-trained with DINO. We use ImageNet-1k [60] ("Inet"), Places205 [84], PASCAL VOC [24] and Oxford-102 flowers ("FLOWERS") [46]. ViT trained with DINO provides features that are particularly \(k\)-NN friendly.
Logistic \(k\)-NN
RN50 ViT-S \(\Delta\) RN50 ViT-S \(\Delta\)
Inet 100% 72.1 75.7 3.6 67.5 74.5 7.0
Inet 10% 67.8 72.2 4.4 59.3 69.1 9.8
Inet 1% 55.1 64.5 9.4 47.2 61.3 14.1
Pl. 10% 53.4 52.1 -1.3 46.9 48.6 1.7
Pl. 1% 46.5 46.3 -0.2 39.2 41.3 2.1
VOC07 88.9 89.2 0.3 84.9 88.0 3.1
FLOWERS 95.6 96.4 0.8 87.9 89.1 1.2
Average \(\Delta\) 2.4 5.6
Table 11: ImageNet classification with different pretraining. Top-1 accuracy on ImageNet for supervised ViT-B/16 models using different pretrainings or using an additional pretrained convnet to guide the training. The methods use different image resolution ("res.") and training procedure ("tr. proc."), i.e., data augmentation and optimization. "MPP" is Masked Patch Prediction.
Pretraining res. tr. proc. Top-1
method data
Pretrain on additional data
MMP JFT-300M 384 [19] 79.9
Supervised JFT-300M 384 [19] 84.2
Train with additional model
Rand. init. - 224 [69] 83.4
No additional data nor model
Rand. init. - 224 [19] 77.9
Rand. init. - 224 [69] 81.8
Supervised ImNet 224 [69] 81.9
DINO ImNet 224 [69] 82.8
Table 12: Low-shot learning on ImageNet with frozen ViT features. We train a logistic regression on frozen features (FROZEN). Note that this FROZEN evaluation is performed without any fine-tuning nor data augmentation. We report top-1 accuracy. For reference, we show previously published results that uses finetuning and semi-supervised learning.
Method Arch Param. Top 1
1% 10%
Self-supervised pretraining with finetuning
UDA [75] RN50 23 - 68.1
SimCLRv2 [13] RN50 23 57.9 68.4
BYOL [30] RN50 23 53.2 68.8
SwAV [10] RN50 23 53.9 70.2
SimCLRv2 [16] RN50w4 375 63.0 74.4
BYOL [30] RN200w2 250 71.2 77.7
Semi-supervised methods
SimCLRv2+KD [13] RN50 23 60.0 70.5
SwAV+CT [3] RN50 23 - 70.8
FixMatch [64] RN50 23 - 71.5
MPL [49] RN50 23 - 73.9
SimCLRv2+KD [13] RN152w3+SK 794 76.6 80.9
Frozen self-supervised features
DINO -FROZEN ViT-S/16 21 64.5 72.2

B. Methodology Comparison

Table 13: Methodology comparison for DEIT-small and ResNet-50. We report ImageNet linear and \(k\)-NN evaluations validation accuracy after 300 epochs pre-training. All numbers are run by us and match or outperform published results.
Method ResNet-50 ViT-small
Linear \(k\)-NN Linear \(k\)-NN
MoCo-v2 71.1 62.9 71.6 62.0
BYOL 72.7 65.4 71.4 66.6
SwAV 74.1 65.4 71.8 64.7
DINO 74.5 65.6 76.1 72.8
Figure 8: Self-attention for a set of reference points. We visualize the self-attention module from the last block of a ViT-S/8 trained with DINO. The network is able to separate objects, though it has been trained with no supervision at all.
Table 14: Relation to MoCo-v2 and BYOL. We ablate the components that differ between DINO, MoCo-v2 and BYOL: the loss function (cross-entropy, CE, versus InfoNCE, INCE, versus mean-square error, MSE), the multi-crop training, the centering operator, the batch normalization in the projection heads and the student predictor. Models are run for 300 epochs with ViT-S/16. We report top-1 accuracy on ImageNet linear evaluation.
Method Loss multi-crop Center. BN Pred. Top-1
1 DINO CE ✓ ✓ 76.1
2 - MSE ✓ ✓ 62.4
3 - CE ✓ ✓ ✓ 75.6
4 - CE ✓ 72.5
5 MoCov2 INCE ✓ 71.4
6 - INCE ✓ ✓ 73.4
7 BYOL MSE ✓ ✓ 71.4
8 - MSE ✓ 0.1
9 - MSE ✓ 52.6
10 - MSE ✓ ✓ ✓ 64.8
Table 15: Relation to SwAV. We vary the operation on the teacher output between centering, a softmax applied over the batch dimension and the Sinkhorn-Knopp algorithm. We also ablate the Momentum encoder by replacing it with a hard copy of the student with a stop-gradient as in SwAV. Models are run for 300 epochs with ViT-S/16. We report top-1 accuracy on ImageNet linear evaluation.
Method Momentum Operation Top-1
1 DINO ✓ Centering 76.1
2 - ✓ Softmax (batch) 75.8
3 - ✓ Sinkhorn-Knopp 76.0
4 - Centering 0.1
5 - Softmax (batch) 72.2
6 SwAV Sinkhorn-Knopp 71.8 
# x is n-by-k
# tau is Sinkhorn regularization param
x = exp(x / tau)
for _ in range(num_iters):  # 1 iter of Sinkhorn
    # total weight per dimension (or cluster)
    c = sum(x, dim=0, keepdim=True)
    x /= c

    # total weight per sample
    n = sum(x, dim=1, keepdim=True)
    # x sums to 1 for each sample (assignment)
    x /= n
x = softmax(x / tau, dim=0)
x /= sum(x, dim=1, keepdim=True)

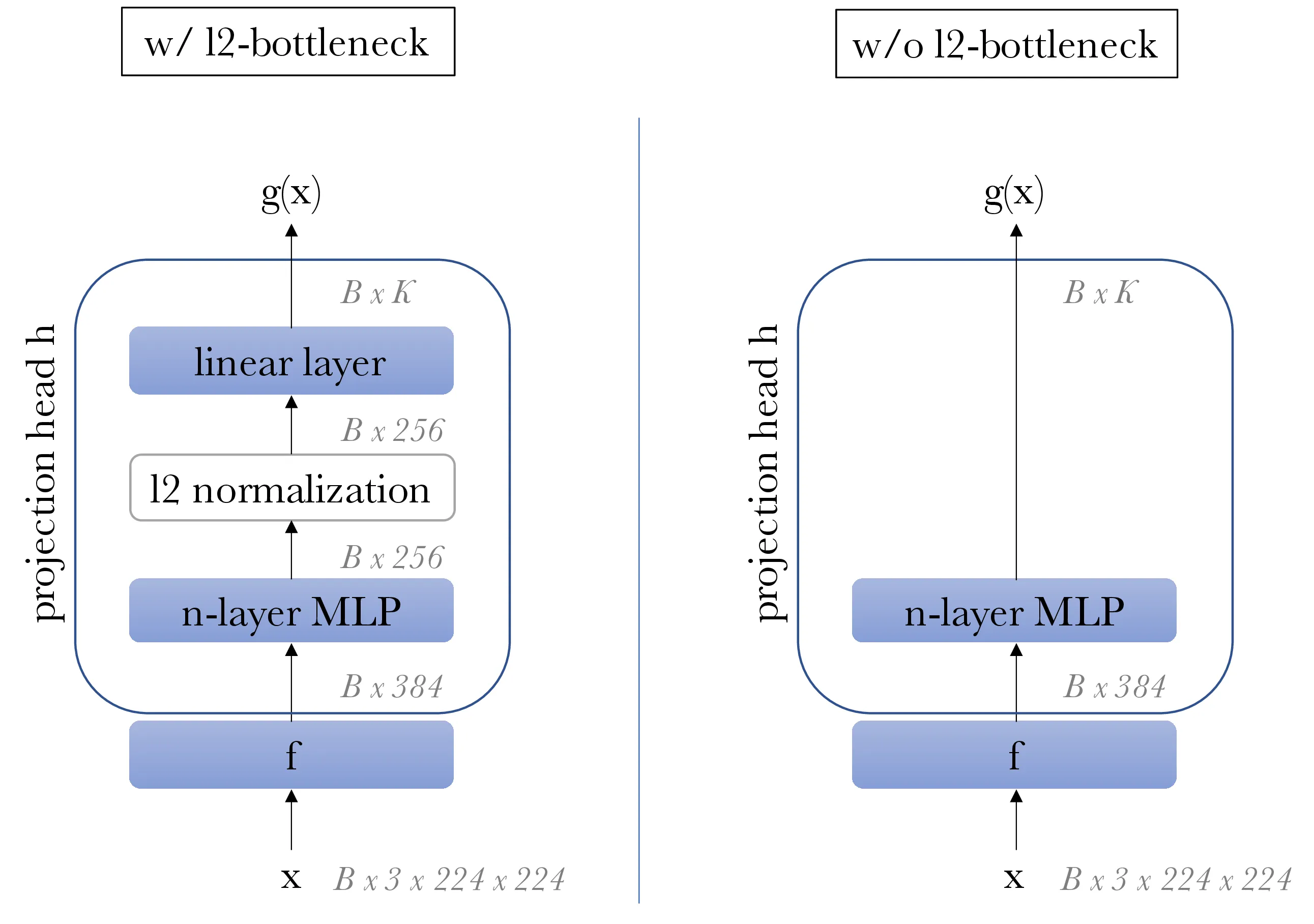
C. Projection Head

ViT-S, 100 epochs heads w/o BN heads w/ BN
\(k\)-NN top-1 69.7 68.6
# proj. head linear layers 1 2 3 4
w/ l2-norm bottleneck - 62.2 68.0 69.3
w/o l2-norm bottleneck 61.6 62.9 0.1 0.1
Figure 9: Projection head design w/ or w/o l2-norm bottleneck.
\(K\) 1024 4096 16384 65536 262144
\(k\)-NN top-1 67.8 69.3 69.2 69.7 69.1
ViT-S, 100 epochs heads w/ GELU heads w/ ReLU
\(k\)-NN top-1 69.7 68.9

D. Additional Ablations

\(m\) 0 0.9 0.99 0.999
\(k\)-NN top-1 69.1 69.7 69.4 0.1
\(\tau_t\) 0 0.02 0.04 0.06 0.08 0.04 \(\to\) 0.07
\(k\)-NN top-1 43.9 66.7 69.6 68.7 0.1 69.7
DINO ViT-S 100-ep 300-ep 800-ep
\(k\)-NN top-1 70.9 72.8 74.5

ViT-S/16 weights
Random weights 22.0
Supervised 27.3
DINO 45.9
DINO w/o multicrop 45.1
MoCo-v2 46.3
BYOL 47.8
SwAV 46.8
# heads dim dim/head # params im/sec \(k\)-NN
6 384 64 21 1007 72.8
8 384 48 21 971 73.1
12 384 32 21 927 73.7
16 384 24 21 860 73.8

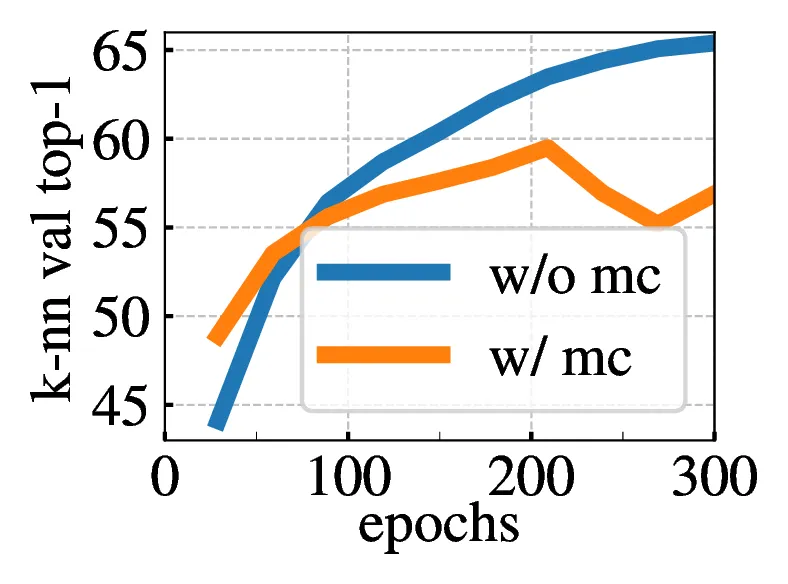
E. Multi-crop

(0.05, s), (s, 1), s: 0.08 0.16 0.24 0.32 0.48
\(k\)-NN top-1 65.6 68.0 69.7 69.8 69.5
crops 2 × 2242 2 × 2242 + 6 × 962
eval \(k\)-NN linear \(k\)-NN linear
BYOL 66.6 71.4 59.8 64.8
SwAV 60.5 68.5 64.7 71.8
MoCo-v2 62.0 71.6 65.4 73.4
DINO 67.9 72.5 72.7 75.9

F. Evaluation Protocols

F.1 \(k\)-NN classification

F.2 Linear classification

concatenate \(l\) last layers 1 2 4 6
representation dim 384 768 1536 2304
ViT-S/16 linear eval 76.1 76.6 77.0 77.0
pooling strategy [CLS] tok. only concatenate [CLS] tok. and avgpooled patch tok.
representation dim 768 1536
ViT-B/16 linear eval 78.0 78.2

G. Self-Attention Visualizations

H. Class Representation

Figure 10: Self-attention heads from the last layer. We look at the attention map when using the [CLS] token as a query for the different heads in the last layer. Note that the [CLS] token is not attached to any label or supervision.
Figure 11: t-SNE visualization of ImageNet classes as represented using DINO. For each class, we obtain the embedding by taking the average feature for all images of that class in the validation set.